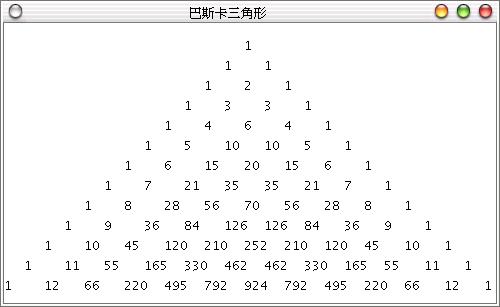
解法
巴斯卡三角形中的 nCr 可以使用以下這個公式來計算,以避免階乘運算時的數值溢位:
nCr = [(n-r+1)/r] * nCr-1
nC0 = 1
nC0 = 1

/* 計算nCr,但是並不快,只是方便 */
Procedure COMBI(n, r) [
FOR(i = 1; i <= r; i = i + 1)
p = p * (n-i+1) / i;
RETURN p;
]
#include <stdio.h>
#define N 12
long combi(int n, int r){
int i;
long p = 1;
for(i = 1; i <= r; i++)
p = p * (n-i+1) / i;
return p;
}
void paint() {
int n, r, t;
for(n = 0; n <= N; n++) {
for(r = 0; r <= n; r++) {
int i;
/* 排版設定開始 */
if(r == 0) {
for(i = 0; i <= (N-n); i++) {
printf(" ");
}
}
else {
printf(" ");
} /* 排版設定結束 */
printf("%3d", combi(n, r));
}
printf("\n");
}
}
int main() {
paint();
return 0;
}
import java.awt.*;
import javax.swing.*;
public class Pascal extends JFrame {
public Pascal() {
setBackground(Color.white);
setTitle("巴斯卡三角形");
setSize(520, 350);
setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
show();
}
private long combi(int n, int r){
int i;
long p = 1;
for(i = 1; i <= r; i++)
p = p * (n-i+1) / i;
return p;
}
public void paint(Graphics g) {
final int N = 12;
int n, r, t;
for(n = 0; n <= N; n++) {
for(r = 0; r <= n; r++)
g.drawString(" " + combi(n, r),
(N-n)*20 + r * 40, n * 20 + 50);
}
}
public static void main(String args[]) {
Pascal frm = new Pascal();
}
}