說明
蒙地卡羅為摩洛哥王國之首都,該國位於法國與義大利國境,以賭博聞名。蒙地卡羅的基本原理為以亂數配合面積公式來進行解題,這種以機率來解題的方式帶有賭博的意味,雖然在精確度上有所疑慮,但其解題的思考方向卻是個值得學習的方式。
解法
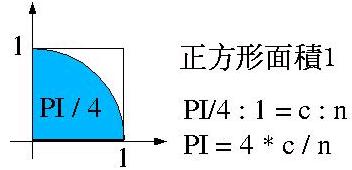
蒙地卡羅的解法適用於與面積有關的題目,例如求PI值或橢圓面積,這邊介紹如何求PI值;假設有一個圓半徑為1,所以四分之一圓面積就為PI,而包括此四分之一圓的正方形面積就為1,如下圖所示:
如果隨意的在正方形中投射飛標(點)好了,則這些飛標(點)有些會落於四分之一圓內,假設所投射的飛標(點)有n點,在圓內的飛標(點)有c點,則依比例來算,就會得到上圖中最後的公式。
至於如何判斷所產生的點落於圓內,很簡單,令亂數產生X與Y兩個數值,如果X^2+Y^2等於1就是落在圓內。
實作
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define N 50000
int main(void) {
int i, sum = 0;
double x, y;
srand(time(NULL));
for(i = 1; i < N; i++) {
x = (double) rand() / RAND_MAX;
y = (double) rand() / RAND_MAX;
if((x * x + y * y) < 1)
sum++;
}
printf("PI = %f\n", (double) 4 * sum / N);
return 0;
}
public class PI {
public static void main(String[] args) {
final int N = 50000;
int sum = 0;
for(int i = 1; i < N; i++) {
double x = Math.random();
double y = Math.random();
if((x * x + y * y) < 1)
sum++;
}
System.out.println("PI = " + (double) 4 * sum / N);
}
}