Algorithm Gossip: 費氏搜尋法

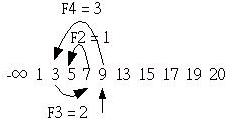
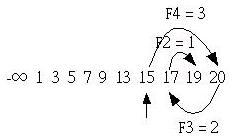
由於第一個搜尋值索引F5 = 5處的值小於19，所以此時必須對齊數列右方，也就是將第一個搜尋值的索引改為F5+2 = 7，然後如同上述的方式進行搜尋，如下所示：

至於第一個搜尋值是如何找到的？我們可以由以下這個公式來求得，其中n為搜尋對象的個數：
 

也就是說Fx必須找到不大於n的費氏數，以10個搜尋對象來說：
 

取F_x = 8, m = 2，所以我們可以對照費氏數列得x = 6，然而第一個數的可能位置之一並不是F6，而是第x-1的費氏數，也就是F₅ = 5。

如果數列number在索引5處的值小於指定的搜尋值，則第一個搜尋位置就是索引5的位置，如果大於指定的搜尋值，則第一個搜尋位置必須加上m，也就是F₅ + m = 5 + 2 = 7，也就是索引7的位置，其實加上m的原因，是為了要讓下一個搜尋值剛好是數列的最後一個位置。

費氏搜尋看來難懂，但只要掌握F_x + m = n這個公式，自己找幾個實例算一次，很容易就可以理解；費氏搜尋除了收斂快速之外，由於其本身只會使用到加法與減法，在運算上也可以加快。

實作

• C

#include <stdio.h> 
#include <stdlib.h> 
#include <time.h> 
#define MAX 15 
#define SWAP(x,y) {int t; t = x; x = y; y = t;} 

void createfib(void);     // 建立費氏數列 
int findx(int, int);          // 找x值 
int fibsearch(int[], int);  // 費氏搜尋 
void quicksort(int[], int, int);  // 快速排序 

int Fib[MAX] = {-999}; 

int main(void) { 
    int number[MAX] = {0}; 
    int i, find; 

    srand(time(NULL)); 

    for(i = 1; i <= MAX; i++) { 
        number[i] = rand() % 100; 
    } 

    quicksort(number, 1, MAX); 

    printf("數列："); 
    for(i = 1; i <= MAX; i++) 
        printf("%d ", number[i]); 

    printf("\n輸入尋找對象："); 
    scanf("%d", &find); 

    if((i = fibsearch(number, find)) >= 0) 
        printf("找到數字於索引 %d ", i); 
    else 
        printf("\n找不到指定數"); 
    
    printf("\n"); 

    return 0; 
} 

// 建立費氏數列 
void createfib(void) { 
    int i; 

    Fib[0] = 0; 
    Fib[1] = 1; 

    for(i = 2; i < MAX; i++) 
        Fib[i] = Fib[i-1] + Fib[i-2]; 
} 

// 找 x 值 
int findx(int n, int find) { 
    int i = 0; 

    while(Fib[i] <= n) 
        i++; 

    i--; 
    return i; 
} 

// 費式搜尋 
int fibsearch(int number[], int find) { 
    int i, x, m; 

    createfib(); 

    x  = findx(MAX+1,find); 
    m = MAX - Fib[x]; 
    printf("\nx = %d, m = %d, Fib[x] = %d\n\n", 
                                     x, m, Fib[x]); 

    x--; 
    i = x; 

    if(number[i] < find) 
        i += m; 

    while(Fib[x] > 0) { 
        if(number[i] < find) 
            i += Fib[--x]; 
        else if(number[i] > find) 
            i -= Fib[--x]; 
        else 
            return i; 
    } 
    return -1; 
} 

void quicksort(int number[], int left, int right) { 
    int i, j, k, s; 

    if(left < right) { 
        s = number[(left+right)/2]; 
        i = left - 1; 
        j = right + 1; 

        while(1) { 
            while(number[++i] < s) ;  // 向右找 
            while(number[--j] > s) ;  // 向左找 
            if(i >= j) 
                break; 
            SWAP(number[i], number[j]); 
        } 

        quicksort(number, left, i-1);   // 對左邊進行遞迴 
        quicksort(number, j+1, right);  // 對右邊進行遞迴 
    } 
} 

• Java

public class FibonacciSearch {
    public static int search(int[] number, int des) { 
        int[] fib = createFibonacci(number.length); 

        int x  = findX(fib, number.length+1, des); 
        int m = number.length - fib[x]; 
        x--; 
        int i = x; 

        if(number[i] < des) 
            i += m; 

        while(fib[x] > 0) { 
            if(number[i] < des) 
                i += fib[--x]; 
            else if(number[i] > des) 
                i -= fib[--x]; 
            else 
                return i; 
        } 
        
        return -1; 

    }
    
    private static int[] createFibonacci(int max) {
        int[] fib = new int[max];
        for(int i = 0; i < fib.length; i++) {
            fib[i] = Integer.MIN_VALUE;   
        }

        fib[0] = 0; 
        fib[1] = 1; 

        for(int i = 2; i < max; i++) 
            fib[i] = fib[i-1] + fib[i-2];
        
        return fib;
    }
    
    private static int findX(int[] fib, int n, int des) {
        int i = 0; 

        while(fib[i] <= n) 
            i++; 

        i--; 
        
        return i;     
    }
    
    public static void main(String[] args) {
        int[] number = {1, 4, 2, 6, 7, 3, 9, 8};
        
        QuickSort.sort(number);
        
        int find = Fibonacci.search(number, 3);
        
        if(find != -1) 
            System.out.println("找到數值於索引" + find); 
        else 
            System.out.println("找不到數值"); 
    }
}