From Gossip@caterpillar

Algorithm Gossip: 八個皇后

說明

西洋棋中的皇后可以直線前進，吃掉遇到的所有棋子，如果棋盤上有八個皇后，則這八個皇后如何相安無事的放置在棋盤上，1970年與1971年， E.W.Dijkstra與N.Wirth曾經用這個問題來講解程式設計之技巧。

解法

關於棋盤的問題，都可以用遞迴求解，然而如何減少遞迴的次數？在八個皇后的問題中，不必要所有的格子都檢查過，例如若某列檢查過，該該列的其它格子就不用再檢查了，這個方法稱為分支修剪。

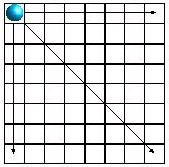
所以檢查時，先判斷是否在已放置皇后的可行進方向上，如果沒有再行放置下一個皇后，如此就可大大減少遞迴的次數，例如以下為修剪過後的遞迴檢查行進路徑：

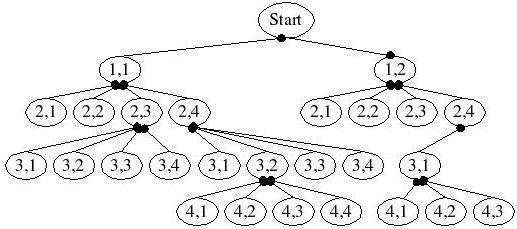
八個皇后的話，會有92個解答，如果考慮棋盤的旋轉，則旋轉後扣去對稱的，會有12組基本解。

實作

#include <stdio.h> 
#include <stdlib.h> 
#define N 8 

int column[N+1]; // 同欄是否有皇后，1表示有 
int rup[2*N+1]; // 右上至左下是否有皇后 
int lup[2*N+1]; // 左上至右下是否有皇后 
int queen[N+1] = {0}; 
int num; // 解答編號 

void backtrack(int); // 遞迴求解 

int main(void) { 
    int i; 
    num = 0; 

    for(i = 1; i <= N; i++) 
        column[i] = 1; 

    for(i = 1; i <= 2*N; i++) 
        rup[i] = lup[i] = 1; 

    backtrack(1); 

    return 0; 
} 

void showAnswer() {
    int x, y;
    printf("\n解答 %d\n", ++num);
    for(y = 1; y <= N; y++) {
        for(x = 1; x <= N; x++) {
            if(queen[y] == x) {
                printf(" Q");
            }
            else {
                printf(" .");
            }
        }
        printf("\n");
    }
}

void backtrack(int i) { 
    int j;

    if(i > N) { 
        showAnswer();
    } 
    else { 
        for(j = 1; j <= N; j++) { 
            if(column[j] == 1 && 
                 rup[i+j] == 1 && lup[i-j+N] == 1) { 
                queen[i] = j; 
                // 設定為佔用
                column[j] = rup[i+j] = lup[i-j+N] = 0; 
                backtrack(i+1); 
                column[j] = rup[i+j] = lup[i-j+N] = 1; 
            } 
        } 
    } 
}

Java

public class Queen {
    // 同欄是否有皇后，1表示有 
    private int[] column;
    // 右上至左下是否有皇后
    private int[] rup; 
    // 左上至右下是否有皇后
    private int[] lup;
    // 解答
    private int[] queen;
    
    // 解答編號
    private int num;
    
    public Queen() {
        column = new int[8+1];
        rup = new int[2*8+1];
        lup = new int[2*8+1];
        
        for(int i = 1; i <= 8; i++) 
            column[i] = 1; 

        for(int i = 1; i <= 2*8; i++) 
            rup[i] = lup[i] = 1; 
        
        queen = new int[8+1];
    }
    
    public void backtrack(int i) {
        if(i > 8) { 
            showAnswer();
        } 
        else { 
            for(int j = 1; j <= 8; j++) { 
                if(column[j] == 1 && 
                   rup[i+j] == 1 && 
                   lup[i-j+8] == 1) { 
                    queen[i] = j; 
                    // 設定為佔用
                    column[j] = rup[i+j] = lup[i-j+8] = 0; 
                    backtrack(i+1); 
                    column[j] = rup[i+j] = lup[i-j+8] = 1; 
                } 
            } 
        } 
    }
    
    protected void showAnswer() {
        num++;
        System.out.println("\n解答 " + num);
        for(int y = 1; y <= 8; y++) {
            for(int x = 1; x <= 8; x++) {
                if(queen[y] == x) {
                    System.out.print(" Q");
                }
                else {
                    System.out.print(" .");
                }
            }
            System.out.println();
        }
    }
    
    public static void main(String[] args) {
        Queen queen = new Queen();
        queen.backtrack(1);
    }
}